What exactly is Temperature ? A statistical picture

What exactly is temperature?, well, Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making up a substance.

This is a type of definition we found normally. Here, I want to show you a view of temperature from the point of view of Statistical Mechanics. So, let's see that,

🪶 Poem

In the realm of particles, both tiny and grand,
Microstates flicker, like grains of sand.
Each tiny movement, a story untold,
In a sea of randomness, both fleeting and bold.

The macrostate rises, a global decree,
A sum of the chaos, for all to see.
Temperature whispers, a silent command,
Guiding the dance, both steady and grand.

Hotter the motion, faster they spin,
A thousand small states, a collective win.
From the micro to macro, the scales align,
In temperature’s grasp, all forces combine.

Introduction to Macrostates and Microstates

To understand what these means, we will see an example.

Consider a box of identical coins(\(5\)). Now, just close the lid of the box and give the box a nice shake. This will shuffle all the coins. Now, if we see inside the box, we will see some of the coins with head(\(H\)) pointing up and some with tail(\(T\)). There are \(2^{5}\) possible configuration.

As we know from probability theory, all of these states are equally likely. So, each state have the probability of \(1/2^{5}=2^{-5}\). We say, each of the configuration a Microstate of the system. See the table below,

No.	Microstate (No. of Heads, \(H\))	Microstate Combination
1	H = 0	TTTTT
2	H = 1	HTTTT
3	H = 1	THTTT
4	H = 1	TTHTT
5	H = 1	TTTHT
6	H = 1	TTTTH
7	H = 2	HHTTT
8	H = 2	HTHTT
9	H = 2	HTTHT
10	H = 2	HTTTH
11	H = 2	THHTT
12	H = 2	THTHT
13	H = 2	THTTH
14	H = 2	TTHTH
15	H = 2	TTTHH
16	H = 3	HHHTT
17	H = 3	HHTHT
18	H = 3	HHTTH
19	H = 3	HTHTH
20	H = 3	HTTHH
21	H = 3	THHTH
22	H = 3	THTHH
23	H = 3	TTTHH
24	H = 4	HHHTH
25	H = 4	HHTHH
26	H = 4	HTHHH
27	H = 4	THHHH
28	H = 5	HHHHH

---

See, here Microstate Combination has \(5\) symbols. The first symbol represent face of first coin, second symbol represent face of second coin and all. So, see serial No. \(16\) (\(HHHTT\) ), there \(1^{st}\), \(2^{nd}\) and \(3^{rd}\) coins are showing heads and last two are showing tails. This exact information of each particle is called Microstate. So, to identify a microstate, we need to identify each coin's state individually.

But do we really do this?, Nope! Normally, we just see the number of heads or tails, i.e., we normally categorize the outcome of this shaking box experiment by simply counting the number of coins which are haeds and which are tails (eg: in No. \(16\) we have \(3\) heads and \(2\) tails). This categorization is called Macrostate.

So, from our table, \(H=2\) and \(T=3\) is a macrostate and under this (from serial no. \(7\) to \(15\)) macrostate, we have \(9\) microstates.

🧠 Defn

A microstate refers to a specific detailed configuration of a system's particles, describing the exact arrangement of all individual components (atoms, molecules, coins, etc.). It accounts for the position, momentum, or other properties of each individual element in the system.
A macrostate refers to the overall, large-scale properties of a system, described by thermodynamic quantities like temperature, pressure, energy, or the total number of heads in a coin toss experiment. Multiple microstates can correspond to the same macrostate.

Let's say, we have \(N=100\) coins in the box. Then,

1. The macrostate of \(50H\) and \(50T\) has \(100!/(50!)^2 \approx 10^{29}\) microstates.

2. The macrostate of \(53H\) and \(47T\) has \(100!/(53!)(47!) \approx 8\times 10^{28}\) microstates.

3. The macrostate of \(100H\) and \(0T\) has \(100!/(100!)(0!) =1\) microstate.

So, the key points we notice is that,

1. The system could be described by a very large number of equally likely microstates.

2. What we actually measure is a property of the macrostate (like number of heads in our example) of the system.

3. The macrostates are not equally likely, the microstates are so. As a result, the macrostate with highest number of microstate is the state of the system. (see the video below from 11:31)

Temperature as a Statistical Artifact

Microstates and macrostates also exist in thermal systems. Just like our coin example, thermal systems have a hidden statistical aspect. To specify a microstate for a thermal system, we would need to know the microscopic configuration of every individual atom in the system, such as their positions, velocities, or energy. In practice, it is impossible to measure the exact microstate of the system.

The macrostate of a thermal system, on the other hand, can be described by measurable quantities like pressure, energy, or volume.

Because of this, we don’t concern ourselves with determining the exact microstate. Instead, we assume that for a system with energy \(E\), there are \(\Omega(E)\) equally likely microstates that the system could be in. This number is normally huge.

Building the system

Suppose, we have two large systems that can exchange energy with each other but they can't exchange energy with surrounding(we the image below).

Let's suppose the energy of the first system is \(E_1\) and for the second one has energy \(E_2\). Although, these two can change, the total energy is conserved, i.e., \(E=E_1+E_2\). Also, remember the microstates of each of these two states are \(\Omega_1(E_1)\) and \(\Omega_2(E_2)\).

📝 Note

This implies that, only knowing \(E_1\) or \(E_2\) can determine all things regarding the system.

The possible number of microstates of the whole system is,

\[ \Omega(E) = \Omega_1(E_1)\Omega_2(E_2) \]

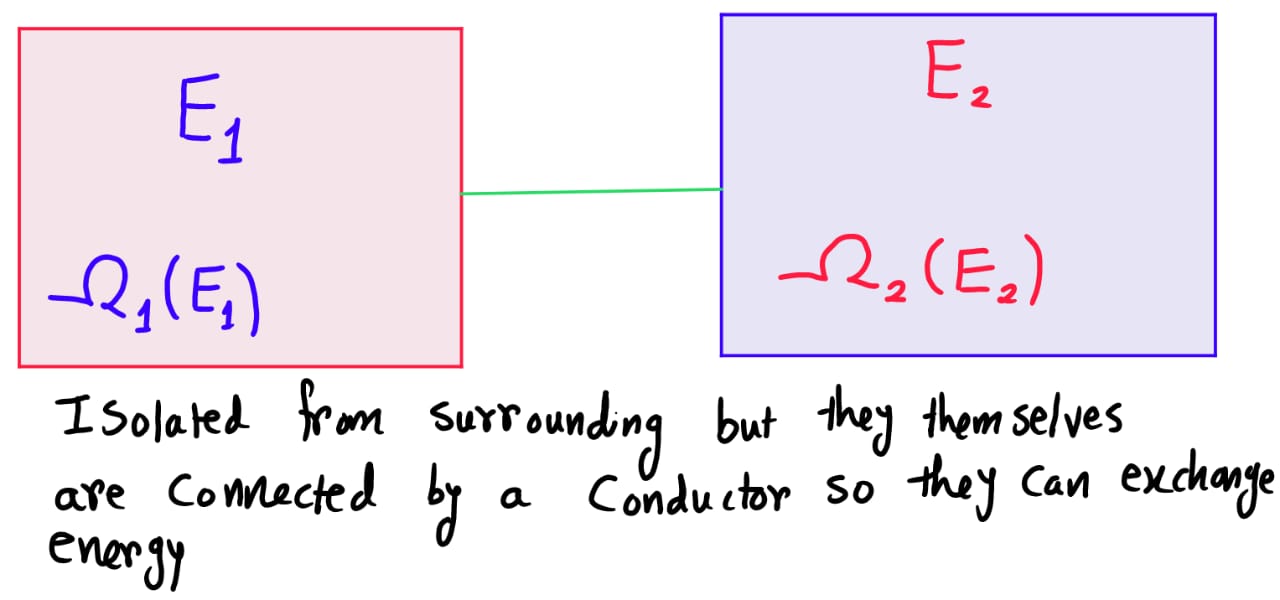
The system can be in anyone of these possible microstates right?... Nope!

Remember, the systems are able to exchange energy with each other and let's assume that they have been left in the condition of being connected together for a sufficiently long time that they have come into thermal equilibrium. This implies, \(E_1\) and \(E_2\) have come to fixed values.

📝 Note

We don't know which one system will choose, we can just say that it will be in a macrostate which maximizes the number of microstates. It should be clearly remembered that, each one of the possible microstates of a system is equally likely. The system's internal interactions, the microstate of the system can continuously change. If we give it enough time, the system will explore all possible microstates and spend an equal time in each of them.

Maximizing microstates and Temperature defn

As previously discussed, the system will choose to maximize the microstate number. So, let's maximize \(\Omega(E_1,E_2)\).

\[ \begin{aligned} \frac{d}{dE_1}(\Omega(E_1,E_2)) &= 0 \\ \Omega_2(E_2)\frac{d \Omega_1(E_1)}{d E_1} + \Omega_1(E_1)\frac{d \Omega_2(E_2)}{d E_2} \frac{d E_2}{d E_1}&= 0 \end{aligned} \]

Using \(dE_1 = - d E_2\), we will have,

\[ \begin{aligned} \frac{1}{\Omega_1(E_1)}\frac{d \Omega_1(E_1)}{d E_1} &= \frac{1}{\Omega_2(E_2)}\frac{d \Omega_2(E_2)}{d E_2} & = \textit{constant}\\ \frac{d \ln(\Omega_1)}{d E_1}&= \frac{d \ln(\Omega_2)}{d E_2} &= \textit{constant} \end{aligned} \]

This condition defines the most likely division of energy between the two systems if they are allowed to exchange energy since it maximizes the total number of microstates. But we know equilibrium means being in the same temperature. So, the constants are function of temperature.

This tells us:

\[ \begin{aligned} \frac{1}{\Omega(E)}\frac{d \Omega(E)}{d E} &= \frac{1}{k T}\\ \frac{d \ln(\Omega(E))}{d E} &= \frac{1}{k T} \end{aligned} \]

where \(k\) is the Boltzmann constant (we will use natural unit, hence setting \(k=1\)).

🧠 Defn

Temperature is number of microstate per unit change of microstate as a result of unit change in energy, i.e., if we change the energy from \(E\) to \(E + dE\), then the system's microstate will also change. The number of microstates of the system per unit change \(d\Omega\) w.r.t \(dE\), gives us temperature.

So, now we have the definition but is that all?, actually yes!

Just using the microstate number, we can find temperature of the system and also see how temp of two system comes to equilibrium.

📝 Note

We can also define entropy using \(\frac{1}{T}=\frac{dS}{dE}\to S = k \ln(\Omega)\). We will not go in too much detail here.

Simulation

Let's use this idea and simulate few models. We will see how the the microstates along can define everything.

We will start with a model where \(\Omega \propto E^3\). Let's first define all the functions we need.

using Random, ForwardDiff
function omega1(E)
    return E^3
end
function omega2(E)
    return E^4
end
function temperature1(E)
    g = x -> ForwardDiff.derivative(x -> log(omega1(x)), x)
    return 1 / g(E)
end
function temperature2(E)
    g = x -> ForwardDiff.derivative(x -> log(omega2(x)), x)
    return 1 / g(E)
end

Now, let's write a function for simulation.

function heat_transfer(E1, E2, steps)
    energies_1 = [E1]; energies_2 = [E2]
    temperatures_1 = [temperature1(E1)]
    temperatures_2 = [temperature2(E2)]
    for step in 1:steps
        δE = 0.1
        if (E1 - δE >= 0) && (E2 + δE >= 0)
            T1 = temperature1(E1)
            T2 = temperature2(E2)
            if T1 > T2
                E1 -= δE; E2 += δE
            elseif T2 > T1
                E1 += δE; E2 -= δE
            end
            push!(energies_1, E1); push!(energies_2, E2)
            push!(temperatures_1, temperature1(E1))
            push!(temperatures_2, temperature2(E2))
        end
    end
    return energies_1, energies_2, temperatures_1, temperatures_2
end

Now, let's run the simulation.

E1 = 10.0; E2 = 5.0
steps = 100
energies_1, energies_2, temperatures_1, temperatures_2 = heat_transfer(E1, E2, steps)
plot(energies_1, label="Energy of Body 1 (E1)", xlabel="Steps", ylabel="Energy", lw=2,title="Energy Transfer between Bodies")
p1 = plot!(energies_2,lw=2, label="Energy of Body 2 (E2)")
savefig(p1, joinpath(@OUTPUT, "plotlytemp_stat01.json"))
plot(temperatures_1, lw=2, label="Temperature of Body 1 (T1)", xlabel="Steps", ylabel="Temperature", title="Temperature Equilibration between Bodies")
p2 = plot!(temperatures_2,lw=2, label="Temperature of Body 2 (T2)")
savefig(p2, joinpath(@OUTPUT, "plotlytemp_stat02.json"))

Let's see the plots: For the energy we can clearly see both bodies's energy are not equal in equilibrium as their specific heats are different (verify that their specific heats are different).

But as expected in their equilibrium, their temperatures are same.

🤔 Problem

Try modifying the code so that we can also plot their microstate number as a function of temperature.

Before ending let's see one more example. Suppose, we have a box of coins and number of heads represent the energy of the system (This is wrong as energy is not constant, but still it will give you some idea for the problem below).

Then, let's write the code:

using Plots;plotlyjs()
function omega(N::Int, k::Int)
    return binomial(BigInt(N), BigInt(k))
end
function temperature(N, k)
    if k == 0 || k == N
        return Inf  # Avoid division by zero at boundaries
    else
        return 1 / (log(omega(N, k + 1)) - log(omega(N, k)))
    end
end
function entropy(N, k)
    return log(omega(N, k))
end

function simulate_coin_toss(N)
    energies = 0:N
    microstates = [omega(N, k) for k in energies]
    temperatures = [temperature(N, k) for k in energies]
    entropies = [entropy(N, k) for k in energies]
    return energies, microstates, temperatures, entropies
end

function plot_results(N)
    energies, microstates, temperatures, entropies = simulate_coin_toss(N)
    p = plot(layout = (3, 1), size = (1200, 1800))
    p = plot!(energies, microstates, lw=2,label="", xlabel="Energy (Number of Heads)", ylabel="Microstates (Ω)", title="Microstates (Ω)", subplot=1)
    p = plot!(energies, temperatures, lw=2,label="", color=:red, xlabel="Energy (Number of Heads)", ylabel="Temperature (T)", title="Temperature (T)", subplot=2)
    p = plot!(energies, entropies, lw=2, color=:green,label="", xlabel="Energy (Number of Heads)", ylabel="Entropy (S)", title="Entropy (S)", subplot=3)
    return p
end

Now, let's plot this:

p = plot_results(50)
savefig(p, joinpath(@OUTPUT, "plotlytemp_stat1.json"))

With this

🤔 Problem

Try doing the same for Einstein Model of solid. If needed read this paper: http://dx.doi.org/10.1119/1.18490.

We can actually use a more fundamental idea called Partition Function and Grand Partition Function but let's just end here for today. If you are cursious why not see few formulas to see the power of partition function?, for that visit this nebo notebook.

---

Hope this helps you in some way. If you like it then share with others if possible.

If you have some queries, do let me know in the comments or contact me using my using the informations that are given on the page About Me.

Go Back