The Period of Reciprocals of Primes (work of William Shanks)
You are reading this blog?, This is (even if it's little) you love maths.
But how much?, Can you invest 3 years just to calculate Reciprocal of Prime numbers?...
Yes or No?
I don't know about you but there was certainly a guy called William Shanks, who have done this.
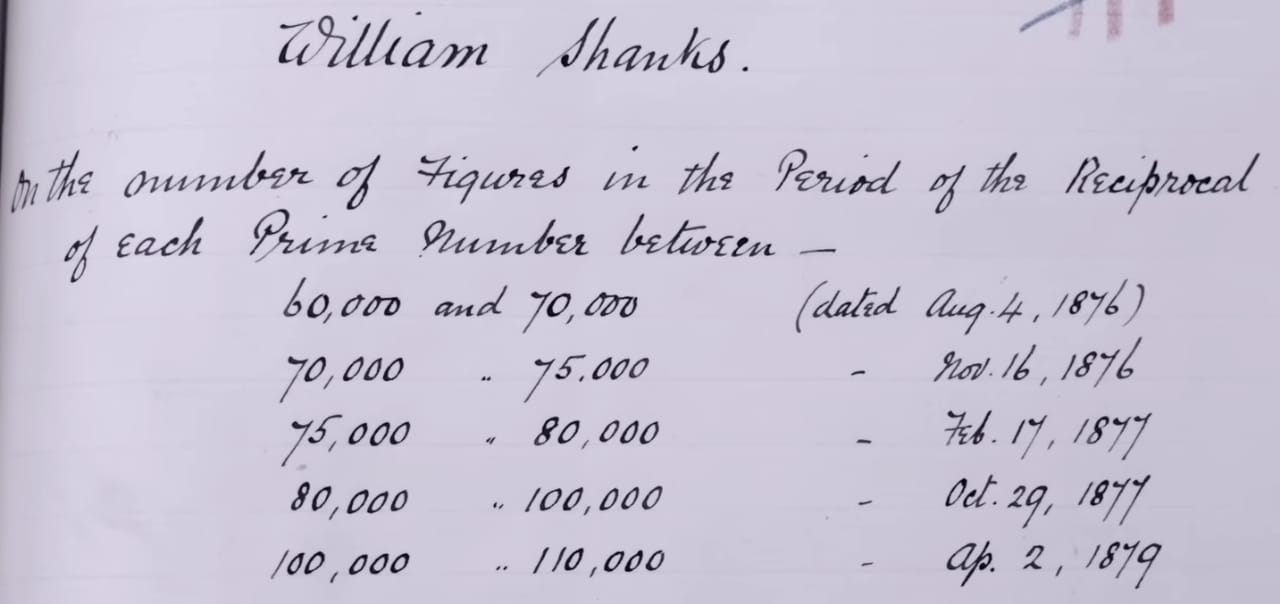
The working period of William Shanks on this topic.
Because, Numbers were the first step in mapping our physical world into abstract one.
Introduction to the problem
Let's first try to undersand what Shanks was doing. Suppose, we have a prime number \(p\). Now, let's calculate the value of \(\frac{1}{p}\).
For an example let's take \(p=7\).
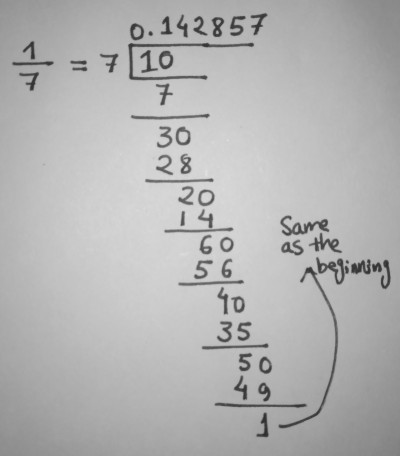
Division of 1 by 7. We all have done this in our childhood. See in the end, we are again getting 1 as we have before.
Hence, The reciprocal of 7 repeats after 6 digits, i.e., It's period is 6.
Why not try the same thing for \(p = 23\)?, What is the period you getting?..
The answer should be 22. Don't skip try this for your own understanding.
Prove
The proof is pretty easy and can be done using Fermat's Little Theorem. For the proof visit this sources.
For more watch this video by Matt Parker Note: p must be a prime greater than 5.
Our take in finding The period
Shanks invested 3 years of his life for this job but in modern time we can just write a few lines of code to achive that in matter of seconds.
I just write it while eating snacks and enjoying a beautiful rainy day... we truly are blessed.. Just think about it!...
If you try finding the code, you are going to find some of them (eg:code-1, code-2). But as per I have seen they have some error or the code looks a bit complicated.
So, I will try to write a code in julia, which will be elegant and simple and also very fast. Let's start will the algorithm.
Algorithm
We want to find the smallest n (\(n=\) no. of digits after which repeatation happens). This simply means that we want to find smallest \(n\) for which
.
For primes \(p\), \(n\) is just some divisor of \(p-1\).
(TRY to THINK WHY)
This means, for any number \(p\), we have to,
Find divisors of \(p-1\).
Then, arrange them in a list of ascending order.
See for which (smallest) n, equation-1 is satisfied.
Let's see an example. Let's take \(p = 23\).
The divisors of \(23-1 = 22\) are \([1,2,11,22]\). For bigger numbers, we will be using a simple code to find the divisors.
using Primes # will be using this library
function divisor(n)
d = Int64[1]
for (p,e) in factor(n)
t = Int64[]
r = 1
for i in 1:e
r *= p
for u in d
push!(t, u*r)
end
end
append!(d,t)
end
return sort(d)
end
println("The divisors of 22 is = ",divisor(22))The output is:
The divisors of 22 is = [1, 2, 11, 22]
The full code for implementing this in julia with an example is,
using Primes # will be using this library
function divisor(n)
d = Int64[1]
for (p,e) in factor(n)
t = Int64[]
r = 1
for i in 1:e
r *= p
for u in d
push!(t, u*r)
end
end
append!(d,t)
end
return sort(d)
end
function period_of_rec_of_prime(p)
divisors = divisor(p-1)
res = 0
for i in divisors
if big(10)^i % big(p) == big(1)
res = i
break
end
end
return res
end
p = 61253
println("The period of $p is = ",period_of_rec_of_prime(p))The output is:
The period of 61253 is = 30626

Few values found by shank. The left ones are prime number and right ones are the periods. As you can see, he had corrected one of the values. Most codes actually give the wrong value but ours will not.
using Primes
using DataFrames
function divisor(n)
d = Int64[1]
for (p,e) in factor(n)
t = Int64[]
r = 1
for i in 1:e
r *= p
for u in d
push!(t, u*r)
end
end
append!(d,t)
end
return sort(d)
end
function period_of_rec_of_prime(p)
divisors = divisor(p-1)
res = 0
for i in divisors
if big(10)^i % big(p) == big(1)
res = i
break
end
end
return res
end
all_primes = primes(7, 110000)#retrun all primes in range 5 to 1,10,000
periods = period_of_rec_of_prime.(all_primes)
df = DataFrame(Primes = all_primes, Reciprocal_Periods = periods)
print(last(df,50))# give table like shank, just showing last 50The output is:
50×2 DataFrame
Row │ Primes Reciprocal_Periods
│ Int64 Int64
─────┼────────────────────────────
1 │ 109441 9120
2 │ 109451 109450
3 │ 109453 9121
4 │ 109469 109468
5 │ 109471 10947
6 │ 109481 7820
7 │ 109507 54753
8 │ 109517 131
9 │ 109519 54759
10 │ 109537 15648
11 │ 109541 21908
12 │ 109547 54773
13 │ 109567 4058
14 │ 109579 15654
15 │ 109583 109582
16 │ 109589 109588
17 │ 109597 54798
18 │ 109609 54804
19 │ 109619 109618
20 │ 109621 109620
21 │ 109639 54819
22 │ 109661 109660
23 │ 109663 36554
24 │ 109673 109672
25 │ 109717 54858
26 │ 109721 54860
27 │ 109741 36580
28 │ 109751 10975
29 │ 109789 109788
30 │ 109793 109792
31 │ 109807 36602
32 │ 109819 109818
33 │ 109829 109828
34 │ 109831 2615
35 │ 109841 6865
36 │ 109843 18307
37 │ 109847 109846
38 │ 109849 27462
39 │ 109859 109858
40 │ 109873 15696
41 │ 109883 54941
42 │ 109891 21978
43 │ 109897 109896
44 │ 109903 109902
45 │ 109913 9992
46 │ 109919 54959
47 │ 109937 109936
48 │ 109943 109942
49 │ 109961 10996
50 │ 109987 54993using Plots
plot(all_primes, periods, title="Plot of Reciprocal of Primes vs Period",seriestype=:scatter,linewidth=3)
xlabel!("Primes")
ylabel!("Period of Reciprocals")This is create a plot like,
I hope you all like this interesting piece of knowlege. Just think how much blessed we are. We should use all our resources(blessings) to do awesome things.
If you have some question, do let me know in the comments or contact me using my using the informations are given in the page About Me.
