What exactly is Light Momentum?
We all of heard many times Light has Momentum!
But the thing is most of us really don't understand why is so or how is responsible for this momentum?
Today in this blog, we will exactly try to understand it from the basic physics. So, just take a cup of tea and get ready.
The ultimate test of your knowledge is your capacity to convey it to another. – Richard Feynmann
Introduction
While studying many topics we have used that fact that, the momentum of light is given by,
\[ p = \frac{E}{c} \]In this eqn-(1), \(E\) represent the energy of light and \(c\) is the speed of light.
Normally, the proof is given by using Einstein Mass-Energy Equivalence formula. The proof is as follows:
Proof:
\[ E^2 = (mc^2)^2 + (pc)^2 \]Now, as light doesn't have any mass, we put \(m=0\), which gives us our expression for the momentum \(p\).
After posting this many people are saying using the \(4-vector\) method , i.e., \(p^{\mu}p_{\mu}\) we can easily find momentum of photon. I guess they have not read the blog. As that method is equivalent to what i just discussed here in this box because
\[ p^{\mu}p_{\mu} = m^2c^2 = \Big(\frac{E}{c}\Big)^2 - \vec{p}\cdot \vec{p} \]The problem with this proof is that fact It doesn't teach us what is physically happening nor it tells us how the hell something which doesn't have any mass can have momentum?
Spolier: Magnetic-Field Component is responsible for Light Momentum
Before exactly learning where is momentum is coming, let's first see if this momentum even exist. In science, we always need experimental evidence to be sure if something really is there.
No matter how beautiful or elegant your theory is if there is no evidence then it's wrong.
So, let's first see the observations. But again before that we have to know what is Momentum?, is it \(mass \times velocity\) or something else?
What is Momentum?
Normally, we say Momentum is a measurement of mass in motion: how much mass is in how much motion. It is usually given the symbol \(\vec{p}\) and it is given by \(\vec{p} = m\vec{v}\). But this is not correct in general.
In many streams of physics, like Analytical Mechanics or Special Theory of Relativity, we have some different expression for momentum. Those expressions boils down to this one in some special case, i.e., \(\vec{p} = m\vec{v}\) is not true in general. Then, what exactly is momentum?
Momentum is a property of any object which tells us it's ability to push or apply force to some other object.
This means even if some object don't have any mass, but if it can push something we can conclude that it has some momentum (just remember \(\vec{F} = \frac{d \vec{p}}{dt}\)). Maybe we will explore this point in much more detail in some future blog.
Evidence of Light's Momentum
Keeping the point of the previous section in our mind, let's see few evidences for light momentum.
Normally when we are sitting in your room while the light is on or maybe sitting outside, you don't feel any push. Then can we say light don't have any mometum?, well no!
Misinformation Alert!!
After posting this, Many people specially Dr. Chentan Waghela, Terry Bollinger pointed out this is clearly a misinformation as the plastic can just fall due to the thermal effect of air and heating, which is 100% correct.
I had added that as it looks visually great. I shouldn't have done that.... Sorry about that. I decided not to remove this part so people can see and understand the mistake.
Maybe it is very small. We have to perform some experiment which can even detect very small momentum. You can actually perform one such experiment in your home with a very strong flash light or a laser(see the video below).

As shown in the video if we took a very light plastic and hit it with a laser, the plasic falls due to the pressure, i.e., force of the light, which implies light can push and hence it has momentum.
An actual visuals to see the pressure of light can be seen in the video below.
Compton effect is actually a very nice proof of light having momentum but we will not discuss that here.
Another nice observation is the tail of Hale Bopp comet. Normally, when a comes goes around it's orbit we expect that it's tail should be tangent to the orbit. But observation showed us it is not the case (see the figure below).
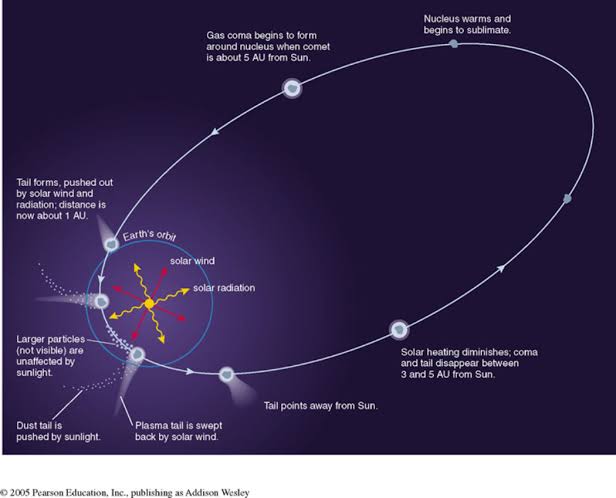
There are many more experiments to notice that light has momentum. If you guys are curious about some experiment to calculate it just go through this paper.
Origin of Momentum of Light
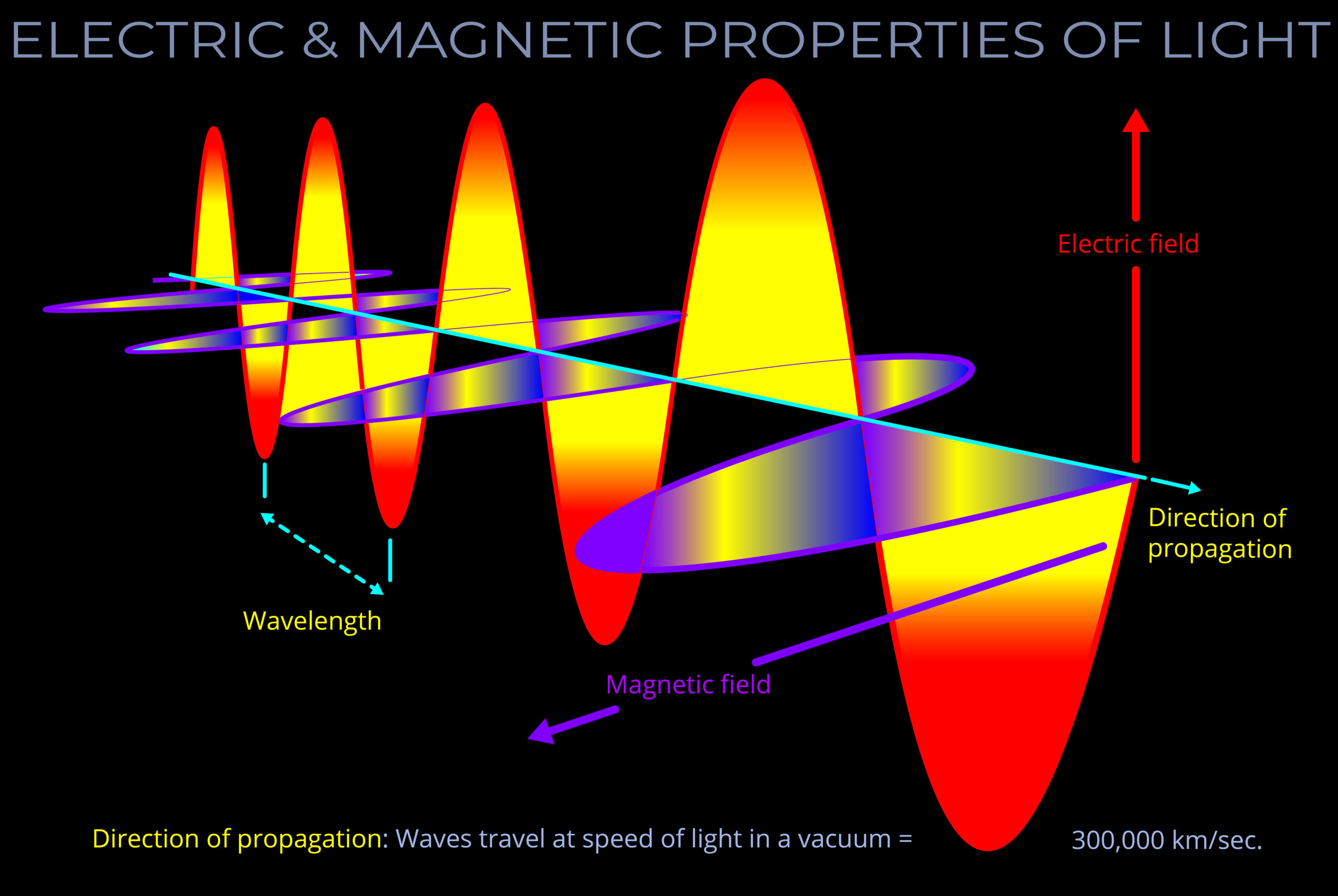
We know Light is a Electro-Magnetic wave. The electric and magnetic field oscillate perpendicular to each other and propagate in the perpendicular direction as shown below.
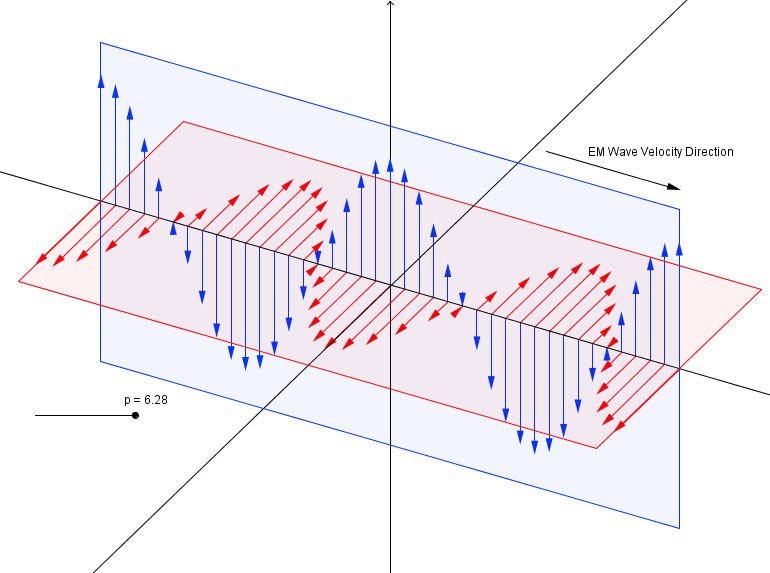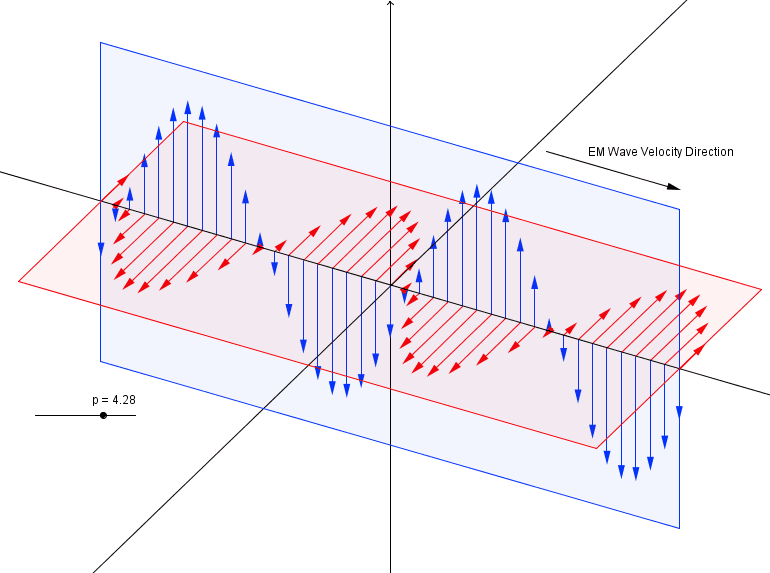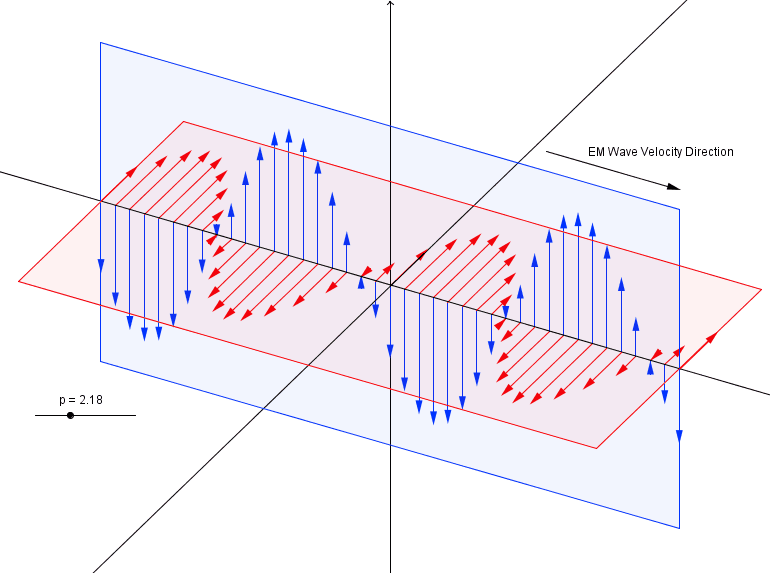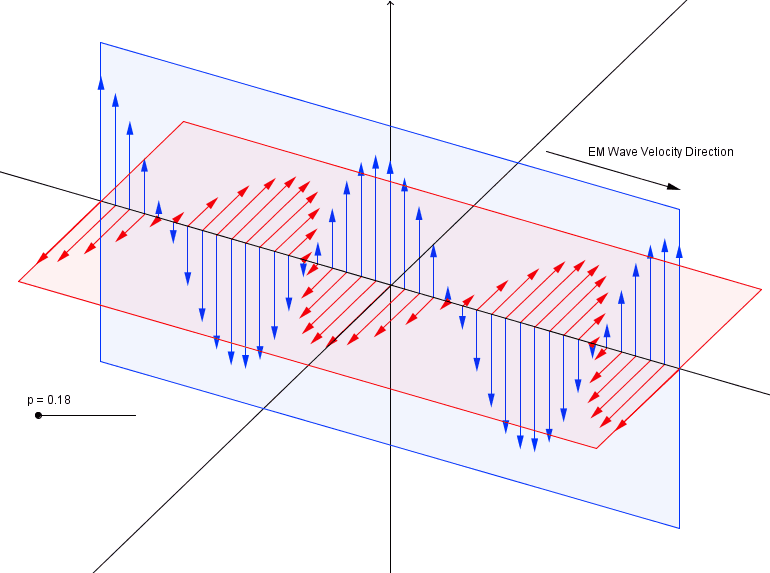
The blue one is electric field and red one is magnetic field.
As shown in the figure, when the E-field points downwards, the electron being an negative charged particle will get pushed upward.
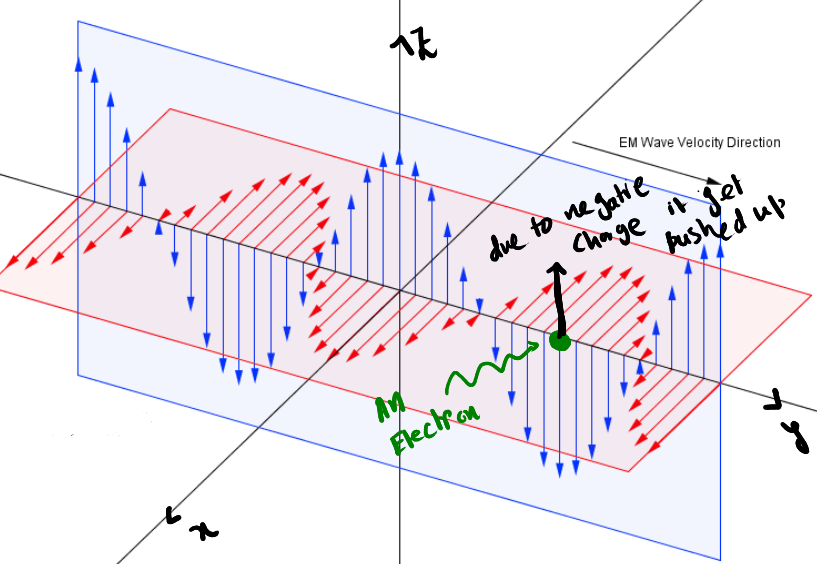
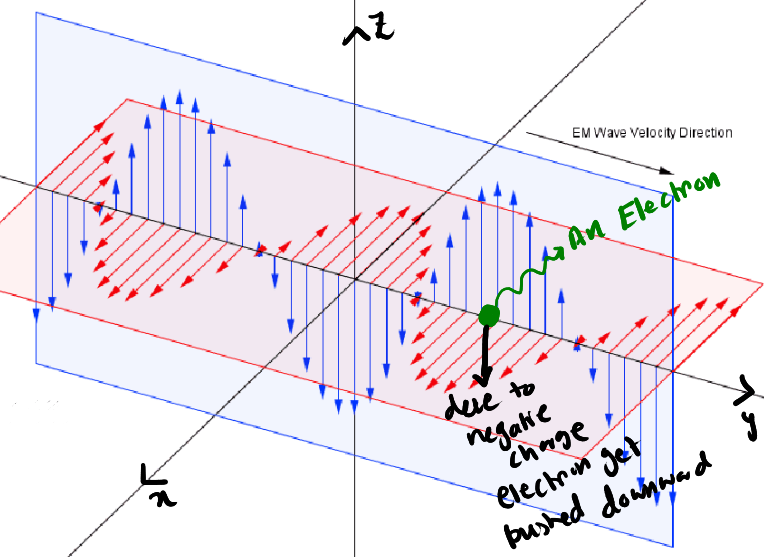
What happens for the case of Magnetic Field?
In this case again let's take an electron at some point. The magnetic field is pointing in the \(-\hat{x}\) direction and due to the electric field the electron will have a velocity in the \(+\hat{z}\) direction.
Using the Lorentz Force equation,
\[ \vec{F}_m = q(\vec{v}\times \vec{B}) \]where \(q\) is the charge of the particle, \(\vec{v}\) is the velocity and \(\vec{B}\) is the magnetic field, we see that the magnetic field will push the electron in the \(+\hat{y}\) direction with a value of \(evB\) (Note: electron has negative charge).
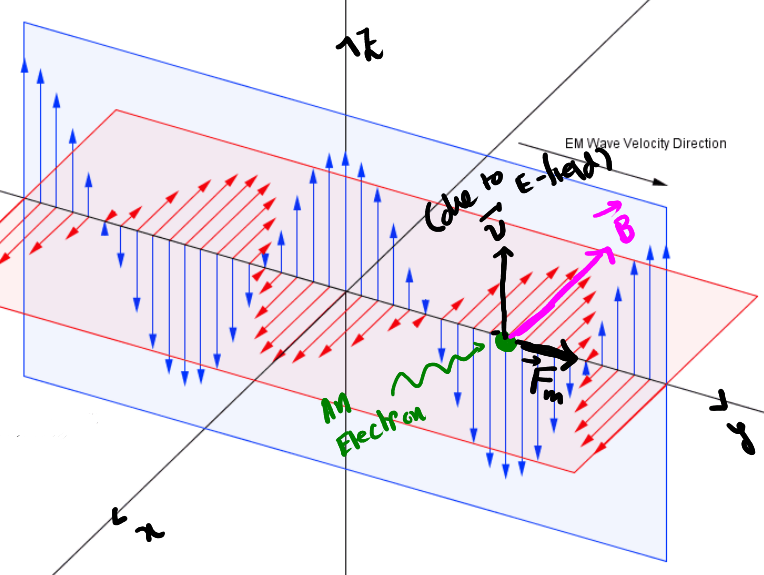
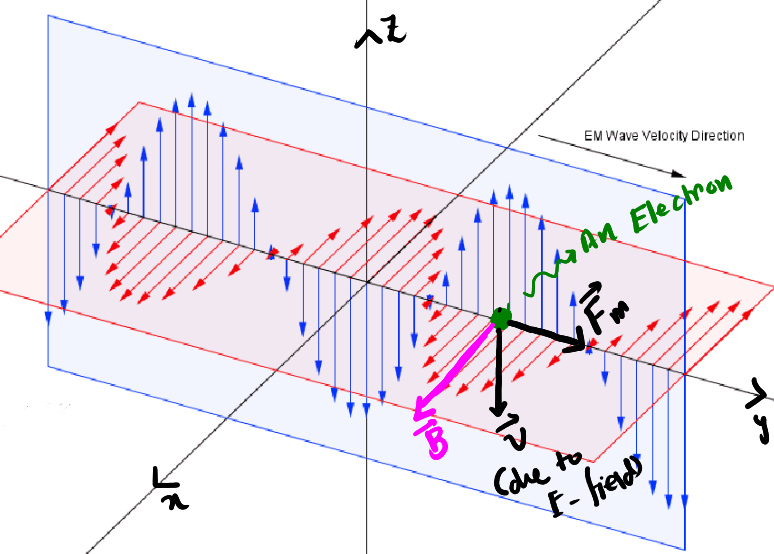
This shows us that Light's momentum is actually provided by the Magnetic Field. So, It is the magnetic field who gives light it's momentum. But if it's true we should be able to derive the eqn-(1). Let's try to derive that.
Proof: The magnetic force on the electron on both case is,
\[ \vec{F}_m = evB \hat{y} \to F_m = evB \]Now, we know that \(B\) and \(E\) follow the relation,
\[ \frac{E}{B} = c \]Using eqn-(6) in eqn-(5) we get,
\[ F_m = \frac{evE}{c} = \frac{vF_e}{c} \]where \(F_e = eE\) is the electric force on the electron.
Note: This tells us that as \(v< c\), Electric Force will always be greater than Magnetic force.
Now, we know the Energy Tranfer per sec(\(E_{enr}/ sec\)) or Power(\(P_{ow}\)) is given by,
\[ P_{ow} = \frac{E_{enr}}{sec} = Fv \]where \(F\) is any force and \(v\) is the velocity of the object of interest.
Using this, we have
As we know Force is rate of change of momentum. Hence, for unit time, we have,
\[ p = \frac{E_{enr}}{c} \]where \(p\) is the momentum transfer done by magnetic field.
Isn't it beautiful?, how we now understand the real physics behind the whole process.
We know understand it is the magnetic field who is giving the momentum, well electric field is also somewhat responsible for this as it gives the initial push giving some velocity to the electrons.
There are few points we should note:
Although the magnetic field is applying the push, the energy stored due in the process is due to electric field. This is the case as magnetic field don't do any work.
The momentum is in the direction to light propagaration. If you consider a proton in place of electron even then it is the case.
I tried my best to explain this, although I am not sure how much you guys have understood but I hope, atleast you have found of insight on this topic.
If you have some queries, do let me know in the comments or contact me using my using the informations that are given on the page About Me.
